
Как и в первом примере, приготовим физическое состояние "f" и при помощи оператора "ameasur" произведем от него некое недерминированное алгоритмическое состояние "a0". Только на этот раз нам понадобятся 2 копии исходного алгоритмического состояния. "a1" и "a2", соответствующие конфигурации системы с двумя открытыми щелями интерферометра. На рисунке ниже приведена программа, соответствующая этому случаю:

Итак, мы имеем 2 начальных идентичных алгоритмических состояния. Предоставим теперь возможность системе развиваться во времени без вмешательства извне. Так как алгоритмическая динамика эргодична, обе алгоритмические точки будут двигаться вдоль одной и той же траектории с некоторым отставанием, соответствующим разности оптических путей или базе интерференции δ. Время t может меняться от 0 до 2n. Программа протоколирует следующую последовательность событий. Первый оператор (строка 1) создает на основе исходного физического состояния "f" начальное алгоритмическое состояние "a1", которое затем дублируется в строке 2. В строках 3и 4 полученные состояния "a1" и "a2" подвергается эволюции со сдвигом по фазе на δ. Далее (строка 5) полученные алгоритмические состояния складываются на поле Галуа и возникшая сумма "a" подвергается измерению (строка 6). В результате получаем некое новое физическое состояние "f1". На рисунке приведен результат расчета по этой программе:
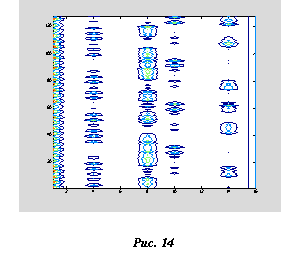
Видно, что диагональная вереница островков трансформировалась в вертикальные полосы. Это означает, что независимо от времени теперь доминируют только определенные физические состояния.
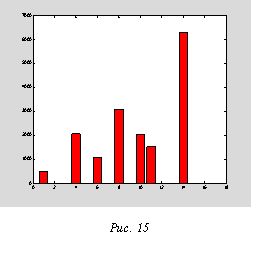
На рисунке 15 приведено распределение по физическим состояниям для этого случая.
Если раньше при измерении в произврольный момент физического времени я мог с равной вероятностью получить любое из 16 физических состояний, то теперь спектр возможных состояний сузился. В результате деструктивной интерференции некоторые состояния стали невозможны, а вероятность других наоборот возросла. Этот результат, действительно, очень напоминает интерференцию в реальных физических системах. Собственно говоря, это и есть интерференция, имеющая место в 7-мерном двоичном пространстве. Мы же наблюдаем проекцию этой интерференции на 4-х мерное подпространство доступное субъекту - наблюдателю.
Равномерная засветка экрана при открытой второй щели стала неоднородной. Аналогичный результат имеет место и при моделировании интерференции в естественной метрике, что еще более эффектно. Действительно, когда мы рассматриваем алгоритмическое движение в естественной метрике, на глаз система совершенно беспорядочно посещают физические состояния (рис. 14). При измерении в любой момент физического времени "частицу" можно обнаружить в любой точке физической координаты. При сложении же двух таких траекторий возникает строго упорядоченный рисунок имитирующий интерференцию.