Моделирование нестационарной интерференции. Движение.

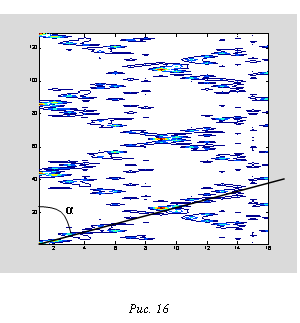
Движение в квантовой механике есть не что иное, как изменение интерференционной картины во времени. Частица, имеющая строго заданный импульс P, не является движущейся в обычном смысле этого слова. Такой квантовый объект стационарен и описывается плоской волной. Этому случаю соответствуют иммитационный эксперимент, описывающийся программой 9 рисунки 9, 10 и 11. В нашей модели он описывается эргодической траекторией алгоритмической точки в конечном двоичном пространстве. Классическое движение в КМ описывается, как изменение во времени и пространстве распределения плотности вероятности. Для этого рассматриваются суперпозиции чистых состояний с разными частотами и фазами. Движение в нашей модели можно получить, складывая разные траектории алгоритмической точки.   На следующем рисунке приведены результаты расчета для этого случая:

Наличие динамики на этом рисунке узнается по наклонной структуре фазовых траекторий с углом α>c_subj=1. Эта траектория соответствуют движению со скоростью меншей скорости света.   

Выводы

По сути дела развиваемая теория субъективной физики по отношению к квантовой механике является  теорией скрытых переменных. Однако, в отличие от теорий такого рода в которых скрытые переменные вводятся формально или ad hoc, у нас они появляются совершенно естественным образом в результате вырождения  физических переменных обусловленного фундаментальной субъективной неполнотой мира. Формально мы рассматриваем конечное пространство (объективную реальность), каждая точка которого сответствует состоянию этого модельного мира. Эти состояния не являются физическими, как и само рассматриваемое  пространство не является физическим объектом. 

Конечность мира, положеннная в основу модели приводит к так называемой физической неполноте. Это означает, что знание субъекта  о  мире не может быть исчерпывающим. Это неполное знание и есть  физическая реальность со свойственной ей квантовой неопределенностью, индетерминизмом и.т.д. Формально мы рассмариваем проекцию нефизического пространства объективной реальности (двоичное конечное пространство) на подпространство физической реальности. В нефизическом пространстве объективной реальности, которое мы иногда называем – алгоритмическим, протекают соответственно и нефизические процессы, которые будучи спроецированы на физическое подпространство дают образы изучаемых нами физических процессов. В настоящей работе мы изучили простейший нефизический процесс – движение точки в  пространстве объективной реальности, подчиняющееся  алгоритму, генерирующему последовательность Грея, что соответствует движению по кратчайшему пути в этом пространстве. Нам удалось продемонстрировать, что проекция этого движения на физическое пространство субъективной физической реальности приводит к  динамике очень похожей на квантовую. При этом проявляются все характерные особенности квантового поведения частицы – нелокальность, индетерминизм при измерениях, волновые свойства.

В связи со сказанным напомним читателю об одном потрясающем по своей красоте и глубине открытии, сделанном первоначально Т. Калуцей и исследованным затем О. Клейном, В.А Фоком, А. Эйнштейном и Ю.Б. Румером. Первоначально было обнаружено, что траектория заряженной частицы может быть строго интерпретирована как геодезическая линия  в  пространстве с расширенной на единицу размерностью. Затем было показано, что соответствующая задача для скалярных частиц может быть сформулирована как задача волновой оптики в пространстве большей размерности. Последующее развитие этих идей привело к созданию теории электрогравитации с некими намеками на обоснование квантовой механики. Незаслуженно редко упоминается формулировка Ю.Б. Румера этой теории , в которой он в качестве дополнительной координаты рассматривал – кординату действия. Следует заметить, что не смотря на значительный прогресс в этом направлении, до сих пор  неясен сам смысл введения дополнительной координаты. В субъективной физике необходимость в дополнительном измерении совершенно естественна. Именно дополнительное измерение  создает здесь слой субъективно скрытых состояний,  возникающих вследствие неустранимой физической неполноты мира. Более того совершенно прозрачен становится смысл так называемого условия цилиндричности, выражающего независимость физических величин по дополнительной координате. Для физического наблюдателя дополнительная координата скрыта и не может обнаруживать себя в явных зависимостях наблюдаемых физических величин. Таким образом, субъективная физика из всех известных формулировок многомерных  теорий позволяет выбрать как единственно верную формулировку  Ю.Б. Румера с пространством координат, времени и действия. Эта формулировка не была принята научной общественностью всерьез по причине конфигурационности пространства    координат, времени и действия. С нашей же точки зрения это является только заслугой теории ибо физическая реальность, будучи субъективной, всегда по своему смыслу скоординирована с субъектом. Абсолютное пространство такая же фикция, как и абсолютная система координат. Заметим, что теория Ю.Б. Румера тем не менее не обосновывает квантовую механику. Она позволяет объяснить каким образом частицы обретают массу, описать квантование масс и в некоторой степени прояснить смысл корпускулярно-волнового дуализма. Однако объяснение специфических  квантовых эффектов остается вне ее возможностей. Она так же как классическая и квантовая механика инвариантна относительно обращения времени.  Все исследователи многомерия от Калуцы до Владимирова[1] в компактифицированные пространства помещали обычные, известные нам - поля. Я же утверждаю, что - поле само является макроскопическим (по сравнению с субквантовым уровнем) проявлением многомерия. Поэтому я рассматриваю движение абстрактной точки в нефизическом компактифицированном пространстве, связанное с обычным физическим пространством посредством специальной процедуры проектирования.

  Процессы в гиперпространстве объективной реальности не обязаны удовлетворять нашим представлениям о физических процессах. Важно только то что бы будучи спроецированы на физическое подпространство они адекватно описывали физику. Естественным следствием нашей модели являются нелокальные квантовые эффекты, нарушающие классическую причинность. Индетерминизм и несимметричное физическое время так же с неизбежностью следуют из нашей модели. Это будет предметом дальнейших публикаций.

 В статье мы не преследовали цель построить модель, описывающую физические процессы на количественном уровне. На данном этапе развития теории это просто невозможно. Однако, нетривиальные качественные результаты, полученные методом компьютерного моделирования для простейшей (7,4) модели служат дополнительным аргументом, вселяющим в нас уверенность, что субъективная физика, построенная на конечном пространстве действительно может служить основой для построения более глубокой модели квантовой реальности.

Приложения:

1. Преобразование Фурье на поле Галуа

Рассмотрим 2 случая. Допустим, источник S генерирует некое чистое КМ состояние ψ(x₁), являющееся  собственным значением оператора координаты. Ему соответствует  измеряемая величина "x₁". Это означает,что на экране свет  всегда будет попадать в одну единственную точку "x₁".  Во втором случае мы воспользуемся другим источником света S, который генерирует суперпозицию всех возможных состояний ψ(x₁),ψ(x₂),ψ(x₃)…, то детектор будет фиксировать свет во всех точках x₁,x₂,x₃...  экрана. Для простоты мы здесь рассматриваем счетное множество состояний.

КМ, следуя традициям классической физики, рассматривает непрерывные спектры собственных функций ψ(x), используя аппарат математического анализа, адаптированный для работы на Гильбертовых пространствах с размерностью, равной мощности континуума.   

Первый случай математически можно описать следующим образом:

                                 (14)

ψ(x) и  ψ(k) связаны посредством линейного преобразования Фурье. Из этого следует, что если  ψ(x) отлична от 0 только при одном значении аргумента x=x₁ , то Спектр функции ψ(k) будет сплошным.  Этот факт известен как соотношение неопределенности для пары сопряженных величин x и p=hk, где k – волновой вектор или пространственная частота. 

Второму случаю соответствует обратное преобразование.

                               (15)

Здесь "x" полностью неопределен и тогда значение k точно фиксировано. Функции  и представляют собой функциональные базисы соответствующих пространств. Говорят о различных представлениях или способах описания процесса.

Аналогичные формулы для дискретного спектра:

     ;                   (16, 17)

Базовые функции  F_kx=  образуют  квадратную матрицу NxN. Выражения же (16, 17) представляют собой линейные преобразования пространства. Запишем их в матричном виде:

X=F_kx * K     ;                K=F_kx * X       (18, 19)

Где X и K – вектора (столбцы) значений функций  ψ(x) и  ψ(k) соответственно. Нас интересует возможность найти аналогичные выражения для конечного двоичного пространства.

Напомним, что мы  рассматриваем 7-мерное двоичное пространство над полем GF(2). Векторами в этом пространстве являются элементы поля GF(2⁷). Алгоритмической (мировой) траекторией в этом пространстве является вектор над полем GF(2⁷). Размерность этого вектора-траектории для поля GF(n^m)  равна  2^m-1. В нашем случае 127. В случае (7,4) модели мы должны использовать матрицы дискретного преобразования над полем Галуа. Воспользуемся базисом Фурье.

Для начала сосредоточим внимание на преобразованиях в физическом слое модельной реальности, то есть преобразованиях  над полем GF(2⁴) и отвлечемся от того, что может иметь место на более глубоком (скрытом) уровне реальности GF(2⁷). Размерность вектора физической траектории в таком пространстве будет 2⁴-1 =15, а размерность преобразующей матрицы 15x15.

Пакет "Matlab" предоставляет широкий ассортимент функций для расчетов на полях Галуа. Продемонстрируем как работает преобразование Фурье на конечном поле.  Рассмотрим простейший пример:

Построим поле Галуа GF(2⁴), воспользовавшись функцией  "gf".

F=gf(0:15,4);                (20)

Получим поле из 16 физических состояний. Примитивным элементом этого поля является третий элемент F(3). Действительно, легко убедиться, что третий элемент является первообразным корнем из единицы этого поля. [F(3)]¹⁵=1. Единицей здесь обозначен единичный элемент F(2) поля.

Далее воспользуемся функцией для построения матрицы дискретного преобразования Фурье.

T = dftmtx(F(3));                      (21)

Воздействуя этой матрицей на вектор, построенный над GF(2⁴), получим вектор в сопряженном представлении. Построим вектор (полином) над полем GF(2⁴),  соответствующий распределению вероятностей на рис 13. Вектор "x", составленный из 15 одинаковых элементов, например F(8)=7 поля GF(2⁴):

x = gf([7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7; 7 ],4)                    (22)

Перейдем в представление пространственных частот [1/x]. или, что то же самое, к импульсному представлению.

y=T*x              (23)

Получим вектор         y=[7;0;0;0;0;0;0;0;0;0;0;0;0;0;0]

Этот тривиальный результат на конечном поле не имеет строгого аналога на континууме. На континууме ему соответствует аксиома или просто определение обобщенной дельта  функции Дирака:

                 (24)

Это равенство также означает, что спектральная плотность постоянного сигнала f(x)=A имеет ненулевое значение только на нулевой частоте. Легко проверить и обратное преобразование. Для этого нужно воспользоваться соответствующей матрицей :

T^-1 = dftmtx(1/F(3));                 (25)

Воздействовав этой матрицей слева на вектор "y" снова вернемся к "x".

x=T^-1 *y                       (26)

Аналогом этого выражения на континууме является :

                  (27)

Так как 7 - нечетное столбцы матрицы T для поля GF(2⁷), образуют эргодические траектории длиной 2⁷..   Преобразование Фурье траектории Грея показывает, что эта функция имеет сложный спектральный состав.

Литература

 [1]  R.Feynman “Simuating Physics with Computers”,Department of physics, California Institute of Technology,Pasadena, California 91107.

2 М.Б.Менский. Успехи физических наук. «Обзоры актуальных проблем. Квантовая механика: новые эксперименты, новые приложения и новые формулировки старых вопросов», Июнь 2000 г., Том 170. № б

3 Клини С.К. Введение в математику с.378.

4 Ф.Л.Бауэр, Г.Гооз. Информатика. перевод с немецкого. Изд. "Мир", М. 1976.

5 Румер Ю.Б. Исследования по 5-оптике. М.:ГИТТЛ, 1956.

Предыдущая    На главную     Следующая