Итак,  независимо от деталей алгоритмической траектории, центр тяжести пучка в среднем "движется" в алгоритмическом пространстве по закону равномерного прямолинейного движения S=c_objt_a так, как если бы двигался некий материальный объект. Где S-номер физического состояния (например, координата), t_a- алгритмическое время, c_obj- величина, по смыслу являющаяся скоростью. Она равна углу наклона α на рисунке 9. Эта скорость равна физическому пути, пройденному за единицу алгоритмического времени. (То есть эта скорость определена в единицах времени объективного наблюдателя). В данном случае скорость с_obj=2^k/2ⁿ=2^k-n равна некоей фундаментальной для данной модели константе, ибо это минимальная скорость. Действительно, в данном случае траектория проходит через все алгоритмические состояния, двигаясь по геодезической. Двигаясь по другой траектории, можно получить только большую скорость. Для (7,4) модели эта скорость равна с_obj=1/8. Таким образом в нашей модели возникает некая универсальная скорость. Это очень важно, так как отражает существование такой скорости в реальном физическом мире.

Рассмотренное движение не есть физическое движение. Это есть фазовое движение. Перемещение плотности алгоритмических точек в бинарном алгоритмическом пространстве эквивалентно кинематическому движению фазы в физическом пространстве. Поэтому, скорости, о которых шла речь выше соответствуют понятию фазовой скорости. Физическая скорость возникает только как проекция на физическое подпространство.

Мы можем значительно упростить модель, если спроецируем ортогональные  физическое k-мерное пространство и скрытое алгоритмическое (n-k)- мерное подпространство на  поверхность тора так, чтобы 2^k физических состояний легли на его большой круг, образуя  пространство физических состояний, а  2^n-k состояний скрытого алгоритмического пространства образовали дополнительное компактифицированное измерение малого круга. В нашем случае это всегда можно сделать восползовавшись известным фактом, что конечное евклидово пространство топологически эквивалентно поверхности тора.  Для нашей (n,k) модели развертка  тора будет выглядеть так как изображено на рисунке 10.

Поверхность разбита на 2ⁿ ячеек, изображающих мировые состояния. Зеленой линией показана  траектория, которой соответствует наименьшая фазовая скорость  и наибольшая скорость физического движения.  В физическом мире обе эти скорости равны скорости света. Желтой линии соответствует траектория такого движения, когда в каждом физическом состоянии система побывала ровно 1 раз. Такая траектория соответствует наибольшей фазовой и наименьшей физической скорости. Это упрощенное представление, конечно нивелирует многие детали реальной алгоритмической динамики, но полезно для понимания того как рассматриваемая модель соотносится с многомерным подходом  типа Клейна - Фока - Румера.

            На следующем рисунке 14  приведены результаты того же эксперимента, что и на рисунке 9, но для естественной метрики. На первый взгляд в этой "криволинейной" системе координат алгоритмическая траектория посещает физические состояния совершенно беспорядочно. Такое движение можно интерпретировать, как происходящее под действием некоторого силового поля, описывающегося соответствующей метрикой (кодировкой). Порядок, соответствующий рисунку 9  может быть легко восстановлен при переходе к старой метрике.

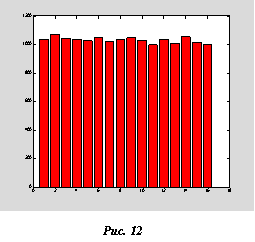
На рисунке 12  дается распределение по физическим состояниям:

Из рисунка видно, что распределение не совсем равномерно. Это вполне естественно и соответствует  флуктуациям света в интерференционных экспериментах с малыми световыми потоками. В нашей модели этот результат "кажущейся" стохастичности для субъективного наблюдателя формально является результатом работы генератора псевдослучайных чисел в операторе "ameasur", при помощи которого приготавливается ансамбль "фотонов".

Физическое движение можно получить, сорганизовав нестационарную интерференцию. Сделать это, можно сложив две или более фазовые траектории разной длины. Тогда с течением времени возникнет фазовый набег, который и обусловит физическое движение. В данном случае удобно рассматривать значительно большие отрезки алгоритмического времени.

 Итак, давайте "откроем" вторую щель нашего модельного интерферометра и посмотрим, что получится. В нашей интерпретации это будет соответствовать двум траекториям точки в конечном пространстве.

 На рис ниже изображен простейший двухщелевой эксперимент. База интерферометра может меняться путем перемещения детектора так как показано на рисунке. Детектор, отмечает факт попадания в него фотона импульсом тока. Средняя величина фототока, очевидно будет пропорциональна вероятности обнаружить систему в данном состоянии "x". Обратите внимание, что мы не говорим о вероятности обнаружить фотон в состоянии с координатой "x", а говорим о целой системе ибо результат измерения зависит от конфигурации системы в целом. Итак, если детектор, закрепленный на координатном столике в положении "x" зарегистрирует фотон, то мы будем говорить, что система была обнаружена в физическом состоянии "x".   

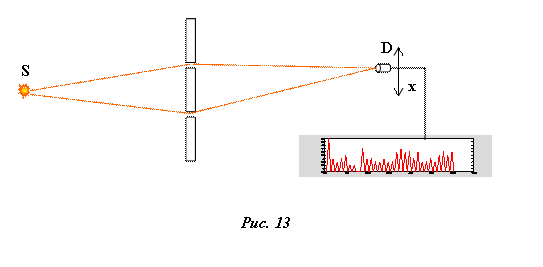
Из  физики известно, что в реальном физическом эксперименте  на экране возникают чередующиеся светлые и темные полосы. Они возникают в результате сложения когерентных волновых полей вероятности, распространяющихся от щелей к экрану. Эти поля, называемые волновыми функциями, вводятся в теорию КМ чисто феноменологически и не имеют референта в физической реальности.

Посмотрим, на что способна наша модель в этом случае.

 Предыдущая    На главную     Следующая