Моделирование движения на конечном поле.
В нашей модели для задания начальных условий нам будет нужна процедура, генерирующая по заданному физическому состоянию на входе произвольное алгоритмическое состояние, лежащее в пределах субъективной ошибки наблюдателя на выходе. Эту процедуру можно сконструировать из оператора антиредукции G, который мы обсуждали выше и специальной рандомизирующей операции "зашумляющей" фазу получившегося вектора алгоритмического состояния таким образом, чтобы ошибка не вывела его за пределы сферы данного физического состояния. По сути эта процедура в некоторой степени обратна процедуре измерения, производящей редукцию вектора алгоритмического состояния к ближайшему физическому состоянию. Эта процедура будет иммитировать подготовку экспериментатором объекта исследования. Назовем эту процедуру "ameasur":
a0=ameasur( f) (8)
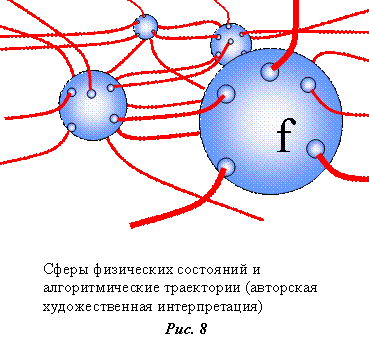
Описание алгоритма этой процедуры также можно найти в приложении. Эта процедура по заданному физическому вектору "f" генерирует некое алгоритмическое состояние "a0", скрытое от наблюдателя. О нем наблюдателю известно только то, что оно лежит в пределах его субъективной ошибки. Если сразу же за процедурой "ameasur" применить процедуру измерения "measur", которую мы так же рассматриваем в приложении, то с вероятностью 1 мы вернемся к исходному физическому состоянию. Этим оператором, например, можно иммитировать испускание одиночных фотонов со случайной фазой. Такой фотон лучше всего ловить сразу же после испускания пока он не "размазался" по всему фазовому пространству. Не зная состояния "a0", мы не можем предсказать дальнейшую эволюцию системы, ибо через сферу физического состояния "f" проходит множество непересекающихся алгоритмических траекторий. Смотрите рисунок.

В результате, начав с неизвестного стартового стояния "a0", принадлежащего данной сфере, через некоторое время траектория окажется внутри сферы другого физического состояния, которое может быть определено только путем измерения. Состояние "а0", конечно, известно нам – объективному наблюдателю, но совершенно недоступно cубъективному. В реальном мире такой ситуации соответствуют эксперименты с одиночными фотонами. Известно, что свет проходя через щель равномерно освещает всю поверхность расположенного за ней экрана. Место попадания одиночного фотона на экран мы в принципе не способны предсказать,- вероятность зарегистрировать фотон в любой точке "x" на поверхности экрана будет одинакова. Можно сказать, что это наилучший генератор случайных чисел, изобретенный самой природой. Наша модель совершенно адекватно описывает этот случай. Этот эксперимент может быть описан следующей последовательностью процедур – операторов.

Оператор "ameasur" мы уже обсуждали. Он подготавливает систему в начальном физическом состоянии с неопределенной для субъективного наблюдателя фазой. Эволюционный оператор "geval" описывает движение системы вдоль траектории Грея. В нашем случае, воздействуя на начальное состояние "a0", он возвращает некое алгоритмическое состояние, в которое придет система через время t. Оператор измерения "measur", воздействуя на текущее алгоритмическое состояние, возвращает физическое состояние, которому оно принадлежит. Таким образом, полностью детерминированный процесс на уровне объективной реальности (в алгоритмическом пространстве) генерирует индетерминированный результат в слое физической реальности. Напомним, что t- здесь алгоритмическое время – число итераций. С физическим временем оно связано весьма необычно. Эта необычность обусловлена проекционным характером этого отношения и приводит к тому, что нулевому или бесконечно малому промежутку физического времени может соответствовать конечный промежуток алгоритмического времени. Необходимо напомнить, что в субъективной физике понятия нуля и бесконечности отличаются от традиционных. Нулевой интервал времени для субъекта вовсе не является объективно нулевым,- это некий конечный интервалл, лежащий в пределах субъективной ошибки. Таким образом, то, что является квантом времени для субъекта объективно имеет длительность, которую можно выразить в единицах времени объективного наблюдателя. Смысл всего этого весьма прозрачен и может быть легко понят. Сделаем пояснения здесь же на месте. Представим, что имеет место некое движение материальной частицы с шагом δx в 10 раз меньшим минимально обнаружимого, тогда любое перемещение этой частицы на x<δx будет расцениваться как покой, ибо у нас нет средств установить движение. И только при x > δx мы можем заметим наличие движения. Величину δx естественно назвать квантом физического пространства. Соответственно δt квантом времени. Важной величиной является полное время вселенной T. Для (n,k) модели это время равно T=2n. Квант времени в этом случае равен δt=2n-k=8 алгоритмическим "секундам" для (7,4) модели.
На рисунке (10) приведена контурная диаграмма, построенная по результатам расчетов с помощью программы (24) в координатах – <физическое состояние – алгоритмическое время>. В данном случае использовалась метрика Грея. Вереница "островов" вдоль диагонали образует траекторию движения системы в физическом подпространстве.
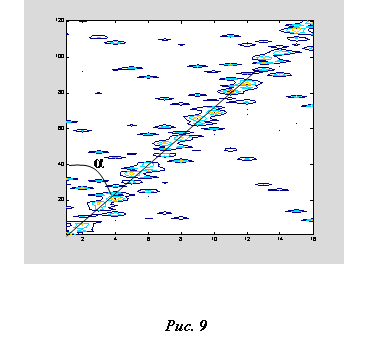
Для того, чтобы получить эту диаграмму программа (24) запускалась для каждого из 128 моментов алгоритмического времени по 100 раз и вычислялось распределение вероятности физических состояний. Алгоритм приведен в приложении.
Из диаграммы видно, что пучок алгоритмических траекторий, берущий начало в одном из физических состояний, не рассеивается по всему пространству и сохраняет свою конфигурацию. В то же время видно, что границы пучка расплывчаты и он как бы пульсирует, переходя от состояния к состоянию. Это означает, что система иногда нелокальным образом (с точки зрения физического наблюдателя) совершает "прыжки" между физическими состояниями. Однако, большую часть времени доминирует движение вдоль диагонали. Это позволяет нам провести следующий анализ.