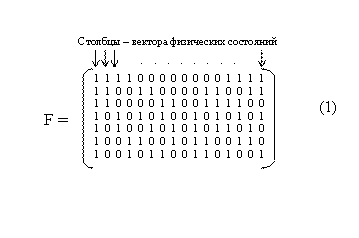
Математическая модель
Рассмотрим m-мерное двоичное пространство, которое будем называть физическим, вложенное в n мерное пространство большей размерности, которое назовем алгоритмическим. Полученную (n,m) структуру будем далее именовать (n,m) - моделью. Следуя предыдущей статье рассмотрим простейший случай n=7, m=4. Тогда пространство нашей модельной объективной реальности будет иметь 128 точек, которым мы будем сопоставлять состояния мира. Итак, каждое состояние нашего модельного мира описывается двоичным 7-вектором. В этом пространстве выберем 16 равноудаленных точек, образующих 8+8 вершин двух пересекающихся 7-мерных симплексов. С каждой такой точкой будут соседствовать еще 7 точек, удаленных от данной точки на расстояние Хемминга h=1, образуя 16 дискретных сфер. Назовем подмножество точек, входящих в такую сферу, физическим состоянием. Матрицу, составленную из векторов, указывающих на центры "физических" сфер, назовем физической.

Легко видеть, что из 16 столбцов этой матрицы только 4 линейно – независимы. Это означает, что каждому физическому состоянию может быть сопоставлен двоичный 4-х вектор. Такого рода структуры хорошо изучены и имеют практическое применение в теории кодирования. Описанная структура представляет собой не что иное, как хорошо известный (7,4) избыточный совершенный код. Напомним, что совершенными или плотно упакованными) называют коды, в которых выполняются соотношения
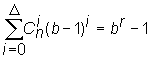
(2)
где Δ - максимальная кратность исправляемых ошибок; b – основание кода r - число проверочных символов. Число известных совершенных кодов ограничено кодами Хэмминга значности
![]()
(3)
и бинарным циклическим кодом Голея. Проблема получения более точных нижних оценок для числа совершенных кодов привлекает внимание математиков давно, однако в полной мере эта задача не решена. Математический аппарат, применяемый в теории избыточных линейных кодов, оказывается пригоден для описания ситуации с физической неполнотой, рассмотренной выше. Вектор физического состояния (кодовое слово) не дает исчерпывающего описания системы, так как это состояние вырождено по соответствующим алгоритмическим состояниям (ошибкам, которые могут быть исправлены). Физическое и алгоритмическое пространства связаны друг с другом проекционными операторами, которые мы будем называть операторами редукции и антиредукции. Оператор антиредукции для (7,4) - модели может быть представлен (n x k) матрицей. Например:
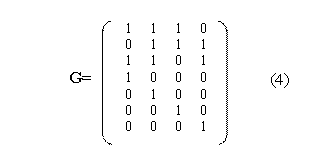
Этот оператор является прямоугольной
матрицей и поэтому воздействуя на 4-x
вектор физического состояния, преобразует его в 7-вектор алгоритмического.
Другими словами он осуществляет восхождение из физического в алгоритмическое
пространство большей размерности.
A=G•F (5)
В теории кодирования такие матрицы используют для генерирования избыточных кодов. Проекционный оператор редукции наоборот понижает размерность вектора, осуществляя "спуск" из алгоритмического пространства в подпространство физической реальности.
F=P•A (6)
Действие этого оператора иммитирует процесс редукции квантового состояния. В теории кодирования этой операцией пользуются для декодирования сообщений. Для совершенных кодов вектор любого алгоритмического состояния мира всегда лежит внутри одной из сфер физических состояний. И механизм действия оператора редукции сводится к определению этой принадлежности.
Компьютерное моделирование (введение)
В этой главе мы будем пользоваться пакетом технических расчетов "Matlab" версии 6.5. Наличие комментариев, поясняющих синтаксис и структуру кода позволят без труда разобраться в нижеследующих фрагментах программ даже тем, кто в области программирования имеет только начальное знание.
(7,4) – модель, которую мы здесь исследуем, конечно, слишком проста и поэтому результаты, которые мы получим будут носить скорее иллюстративный характер. Тем не менее эта простейшая модель позволяет продемонстрировать все основные идеи субъективной физики. Этим мы теперь и займемся.
Для начала получим все физические состояния модели (7,4) при помощи процедуры "getphis", генерирующей матрицу физических состояний:
F=getphis(n) (7)
Эта процедура, конечно, не относится к числу стандартных процедур "Matlab" и написана специально для наших целей. Код процедуры приводится в приложении. Здесь n=7 – размерность двоичного афинного пространства, построенного над полем Галуа GF(2n). Процедура возвращает физическую матрицу (1). Например, физическому состоянию номер 3 будет соответствовать третий столбец физической матрицы f(3)= F(:,3); Мы следуем нотации принятой в "Matlab", в которой двоеточие здесь обозначает – все строки.
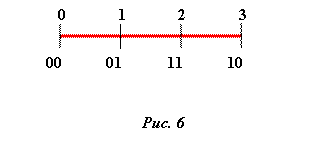
В статье "Субъективная механика" мы показали, что в механике, построенной на конечных полях может быть сформулирован принцип минимума аналогичный принципу Лагранжа в механике. Легко видеть, что кратчайшей траекторией, соединяющей 2 точки в двоичном пространстве, является траектория, полученная на основе кода Грея. Будем называть такую траекторию – траекторией Грея. В дальнейшем нам будет удобнее пользоваться нумерацией точек алгоритмического пространства соответствующей коду Грея. Действительно, почти всегда удобнее работать в системе координат с такой метрикой, в которой геодезические линии являются прямыми. Напомним, что кодировка Грея отличается от позиционной нумерации тем, что соседние числа в ней отличаются всегда только в одном разряде[1]. Метрические свойства нашей модели, таким образом, оказываются жестко привязанными к самим числам. Это иллюстрирует следующий рисунок:
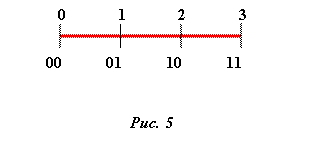
На этом рисунке все отрезки 0-1, 1-2, и 2-3 – равны. Тогда как в метрике Хемминга отрезок 1-2 в 2 раза длиннее отрезка 0-1 и отрезка 2-3. (Напомним, что расстоянием Хемминга между двумя точками называется число, равное числу различий в соответствующих двоичных разрядах). Если мы хотим, чтобы картинка, приведенная выше, выглядела правильно в метрике Хемминга, мы должны перенумеровать точки пространства в соответствии с кодом Грея (выбрать более удобную метрику).
Кроме упомянутых особенностей код Грея порождает последовательность чисел, обладающую фрактальным подобием, что так же весьма привлекательно в связи с требованием самоподобия субъект-объектной структуры мира, которую мы обсуждали выше. На следующем рисунке показана "траектория" образованная последовательностью натуральных чисел в кодировке Грея.
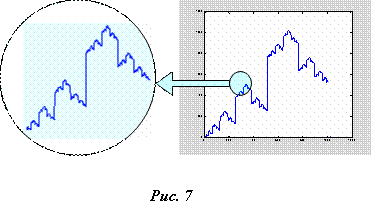
По оси абсцисс отложены натуральные числа, а по оси ординат значение этих чисел в кодировке Грея.
Для того, чтобы проанализировать свойства нашй модели удобнее всего привязаться к конкретному физическому процессу. Казалось бы, что может быть проще движения свободной частицы? Однако, как следует уже из квантовой механики любое движение – это нестационарный прцесс и возниккает в результате сложения и интерференции волн с разными периодами. Поэтому, наша модель прежде всего должна правильно описывать интерференцию.